
6年生の算数で、「角柱と円柱の体積」という単元があります。基本的には「底面積×高さ」が分かっていれば解ける問題です。子どもたちがどのような考え方をしたか、記録しておこうと思います。
基本問題
基本の問題は以下の3つです。
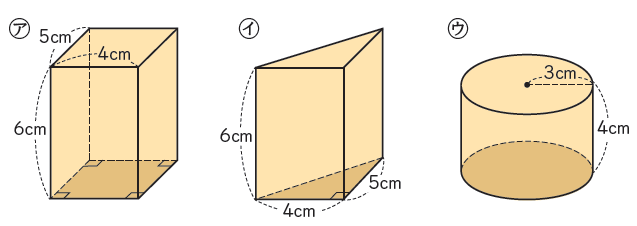
(ア)は四角柱、(イ)は三角柱、(ウ)は円柱です。
これらは全て、「底面積×高さ」という公式で体積を求めることができます。
底面積とは、底面の面積のこと。
(ア)で言えば、5×4=20㎠です。これは高さが1㎤の立体になると、20㎤となります。高さ1単位分の立体の体積は、面積を表す数字と同じになるのです。これが何段あるか、という考え方です。
「底面積が何段分あるか」、これが基本の考え方となります。
応用問題
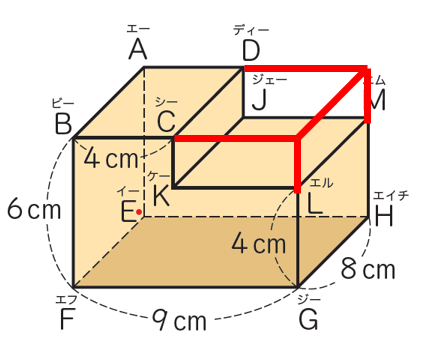
応用問題として教科書に挙げられている問題が以下のものです。
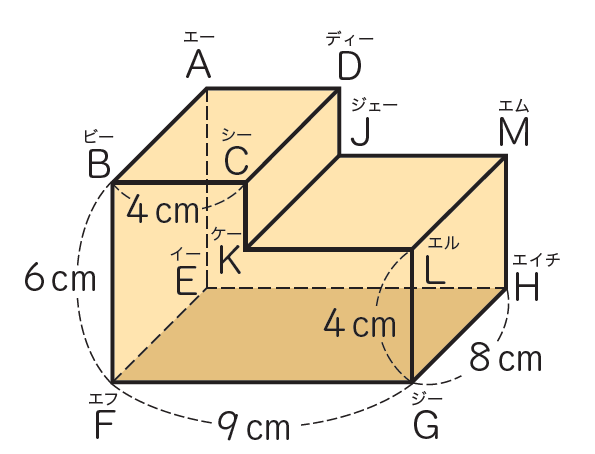
子どもたちがどのように攻略したと思いますか?
立体を分断する。
まず考えられるのは立体を分断する方法です。
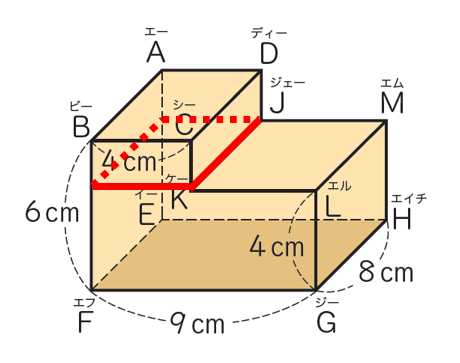
上下に分断したり…
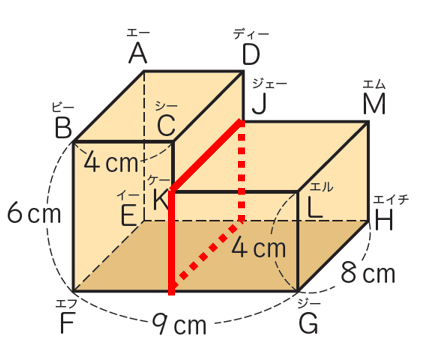
左右に分断したり…
分断してシンプルな四角柱を創り出す方法ですね。
立体を大きく見る
続いては、立体を大きく見る方法。
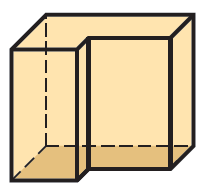
右上のへこんでいる箇所を一時的に埋めて、大きな四角柱として計算します。
後で、一時的に埋めた箇所を引けば答えが出せます。これも分かりやすい考え方です。
向きを変える
教科書には向きを変える方法が載っていました。
向きを変えて、L字になっている部分を底面積としてみるのです。
この方法の利点は「×高さ」を計算するのが1度で済むことです。
分断したり、大きく見たりする方法だと、全ての箇所を立体として計算する必要があります。
しかし、向きを変える方法なら、底面積を求めたの後にまとめて「×高さ」をするだけで済みます。
計算は少ない方がミスも減るので、良い方法だと思いました。
子どもの中でこの方法を自分で書いてきたのは1名のみでした。
見方を変えるって、簡単には思いつきませんよね。
まとめ
様々な形の体積の求め方。覚えることは少ない分、多少の発想力が求められます。
①分断する ②大きく見る ③向きを変える
それぞれの方法の利点を踏まえ、全て使いこなせる上で、自分はどれを使って問題を解くのかを選べる状態にできたらいいなと思いました。




コメント