6年生の算数、最後の新出単元は「データの調べ方」です。私が小学生のときは扱っていなかった学習内容です。大学受験の移行措置とかで初めて現れたような気がします。かなり新鮮な気持ちで臨みました。教科書通りに進めました。今回は、この単元で新しく登場した表やグラフについて簡単にまとめていきます。
課題
簡単に言うと、長縄大会の優勝チームを予想するという問題です。
過去の練習データをもとに、3クラスの記録を比べるのです。
1組の表だけ載せておきます。

2組と3組は、練習日数が異なります。
単純には比べられないぞ、というところから単元がスタートです。
既知の比べ方を復習
まずは、今までで学習してきた内容をもとに優勝チームを予想しました。
子どもたちからは「最多回数で比べる」「平均を出して比べる」等が挙がりました。
教科書にも同じような手順で示されています。
最多回数や最小回数を調べたり、平均を計算したりして求めました。
「集団のデータの平均を、集団のデータの平均値という」と書かれており、ここで「平均値」という言葉を使えるようになりました。
ドットプロット
まず、新登場したのが「ドットプロット」です。

数直線の上に、データをドット(点)で表した図。
上のドットプロットでは、1日目=①、2日目=②、…のように表されています。
また、最も多く出てくる値を「最頻値」と言います。
例えば、上の図の最頻値は61回です。
度数分布表
続いて登場したのは、度数分布表です。
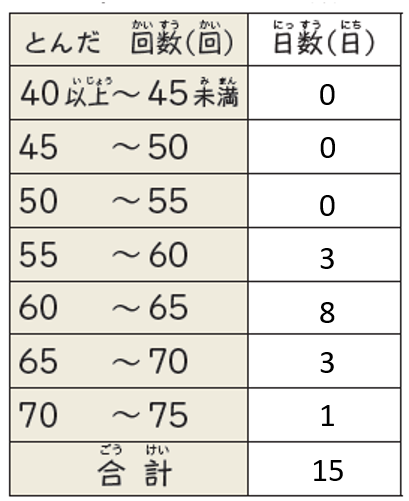
これは、データをいくつかの階級に分けて整理した表です。
ここで用語を整理します。
※階級…データを整理する為に用いる区間
※階級の幅…区間の幅
※度数…各階級に入っているデータの個数
例えば上の度数分布表で見ると…
「55回以上60回未満の階級の度数は、3日です」
「また、階級の幅は5回です」
と言うことができます。
ヒストグラム
次はヒストグラムです。別名「柱状グラフ」と言います。
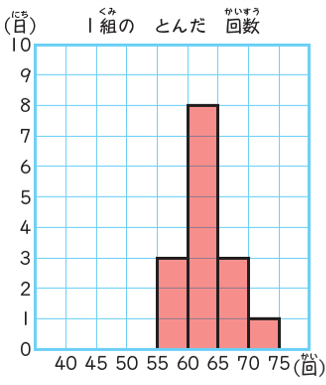
全体の散らばりの様子が一目でわかるのがメリットです。
棒グラフと違い、横軸のメモリ数値と数値の間に棒があります。
度数分布表の考え方を、棒グラフで表したようなものですね。
まとめ
今回は、算数「データの調べ方」で新登場したグラフや図を紹介しました。
授業では、表を見ながら実際に手を動かして書いたり、読み取ったりしました。
私自身も初めて知ることが多く、興味深かったです。




コメント