算数では、比例と反比例の学習をしてきました。学習のポイントとしては、伴って変わる2つの数の関係を、式とグラフに変えられるようなること。中学以降で「関数」の学習に繋がっていく大切な単元です。単元の様子と要点を簡単に記しておきます。
表から考える
比例の表
比例関係にある二つの数を表した表として、下の表が教科書に使われています。

これに矢印を書き入れながら、関係性を調べていきました。
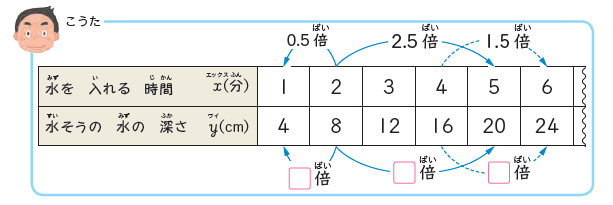
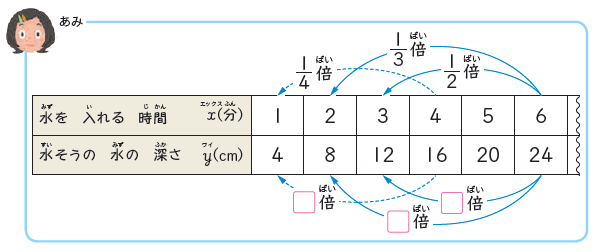
上の「こうたさん」と「あみさん」の四角の中に数を当てはめながら、「比例の決まり」を見つけます。
比例の決まりとしては「一方が□倍になると、もう一方も□倍になる」というものです。
さらに、「□には、整数以外に小数や分数が入ることもある」という決まりがあることも判明しました。
反比例の表
ある程度、比例の学習が済んだところで反比例に入りました。
反比例の例として登場する表は以下のものです。
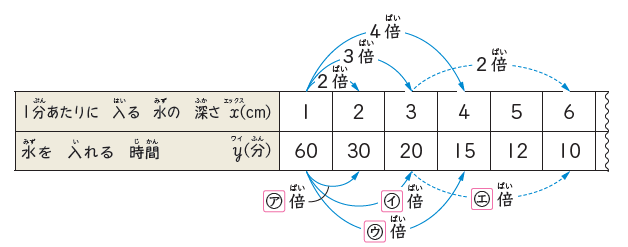
表の(ア)から(エ)の四角を埋めながら、「反比例の決まり」を考えます。
先に判明している「比例の決まり」の文を例示しながら考えさせました。
すると、子ども自ら発言してきます。
「一方が□倍になると、もう一方は1/□倍になる」が正解です。
式にする
比例の式
比例関係にある2つの数は、式に表すことができます。

先程考えた上の表のxとyの数を使って「決まった数」を導きます。
xとyは、どれも「y÷x=4」の関係になります。
つまり「4という決まった数がある」と言えます。
y=4×x。これが今回の表を式にしたものです。
この「決まった数」を使って、比例関係を公式にします。
比例関係にあるものは「y=決まった数×x」という式にすることができます。
6年生は、これを覚えておくのです。
反比例の式
では、反比例はどのような式になるのでしょうか。
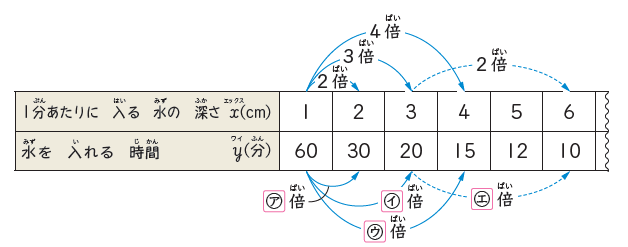
比例の時と同様に、xとyの関係から決まった数を導きます。
すると、どれも「x×y=60」になることが分かりました。
だから、60が「決まった数」になるのです。
y=60÷x。これが今回に反比例の式になります。
反比例の公式としては、「y=決まった数÷x」となると言えるでしょう。
中学では分数にして、「y=a/x」と書きますね。
グラフにする
比例のグラフ
比例関係にあるものは、グラフでかくことができます。
表を見ながら、xとyのぶつかる点をとっていき、全てを結ぶのです。
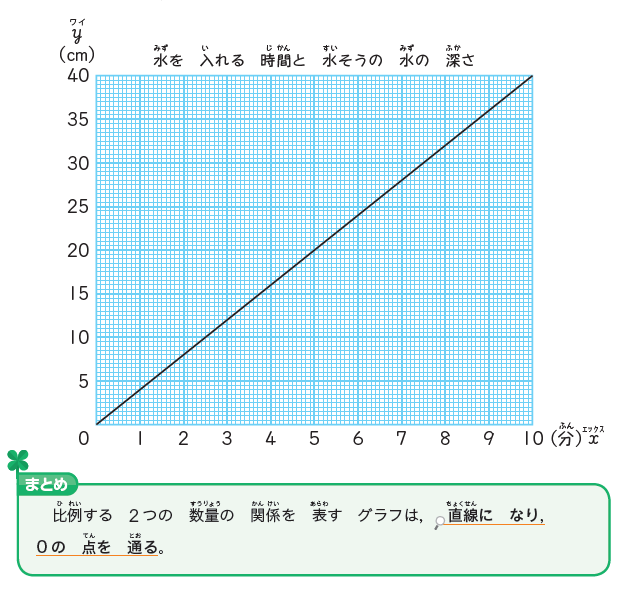
すると、上のような右肩上がりの直線が現れます。
これが比例のグラフです。
決まった数に「ー(マイナス)」がついていない限りは、必ず右肩上がりの直線になるのです。
反比例のグラフ
子どもたちには、まず予想させました。
T「比例は右肩上がりの直線だったけど、反比例の場合はどうなると思う?」
すると、知っている人もいるので「カーブしながら右に下がっていく」という意見が挙がりました。
グラフに点をとって検証します。
予想で挙がった意見通り、右下がりのカーブが現れます。
ただ、子どもたちは点と点を直線で結びたがるので、揺さぶり発問を入れます。
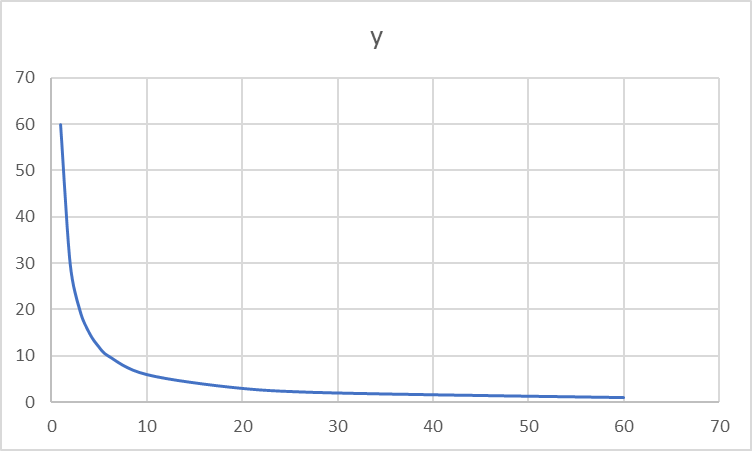
T「これは本当に直線で引いていいの?」
ほとんどの子どもが「直線で引いた方がいい」と答えたので、私から説明を加えました。
反比例のグラフは直線で引けません。
カーブを描くはずなのに途中を直線でかいてはいけませんね。
教科書にも、点を書くまでで終わっています。
子どもたちにそれをそう話すと、驚きの声が上がりました。
まとめ
比例と反比例は、表や式、グラフといった流れで系統立てて考えると分かりやすくなります。
逐一、比例ではどうだったか? 反比例ではどうだったか? と比べていくことで違いを整理しながら進めることができました。
テストでもきちんと点数を取らせてあげられるよう、明日の確認問題ページも抜かりなく進めていきたいと思っています。
ちなみに…
上に張り付けた反比例のグラフはエクセルを使って自作しました。
面白かったし、多少の達成感もあったので、子どもたちにも教えてあげたいです。



コメント